
-l <depth>
-f <depth>
-sh <boolean>
-otl <boolean>
-esp <boolean>
-fsp <level>
-block <boolean>
-strides <boolean>
-compilable <value>
-callable <boolean>
-o <output>
--help or -h
--version or -v
--quiet or -q
This manual is for CLooG version {No value for `VERSION'}, a software which generates loops for scanning Z-polyhedra. That is, CLooG produces a code visiting each integral point of a union of parametrized polyhedra. CLooG is designed to avoid control overhead and to produce a very efficient code.
It would be quite kind to refer the following paper in any publication that results from the use of the CLooG software or its library:
@InProceedings{Bas04,
author = {C. Bastoul},
title = {Code Generation in the Polyhedral Model
Is Easier Than You Think},
booktitle = {PACT'13 IEEE International Conference on
Parallel Architecture and Compilation Techniques},
year = 2004,
pages = {7--16},
month = {september},
address = {Juan-les-Pins}
}
Copyright © 2002-2005 Cédric Bastoul.
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 published by the Free Software Foundation. To receive a copy of the GNU Free Documentation License, write to the Free Software Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA 02111-1307 USA.
CLooG is a free software and library generating loops for scanning Z-polyhedra. That is, it finds a code (e.g. in C, FORTRAN...) that reaches each integral point of one or more parameterized polyhedra. CLooG has been originally written to solve the code generation problem for optimizing compilers based on the polytope model. Nevertheless it is used now in various area, e.g., to build control automata for high-level synthesis or to find the best polynomial approximation of a function. CLooG may help in any situation where scanning polyhedra matters. It uses the best state-of-the-art code generation algorithm known as the Quilleré et al. algorithm (see Qui00) with our own improvements and extensions (see Bas04). The user has full control on generated code quality. On one hand, generated code size has to be tuned for sake of readability or instruction cache use. On the other hand, we must ensure that a bad control management does not hamper performance of the generated code, for instance by producing redundant guards or complex loop bounds. CLooG is specially designed to avoid control overhead and to produce a very efficient code.
CLooG stands for Chunky Loop Generator: it is a part of the Chunky project, a research tool for data locality improvement (see Bas03a). It is designed also to be the back-end of automatic parallelizers like LooPo (see Gri04). Thus it is very compilable code oriented and provides powerful program transformation facilities. Mainly, it allows the user to specify very general schedules where, e.g., unimodularity or invertibility of the transformation doesn't matter.
The current version is still under
evaluation, and there is no guarantee that the upward compatibility
will be respected (but the previous API has been stable for two years,
we hope this one will be as successful -and we believe it-).
A lot of reports are necessary to freeze the library
API and the input file shape. Most API changes from 0.12.x to 0.14.x
have been requested by the users themselves.
Thus you are very welcome and encouraged
to post reports on bugs, wishes, critics, comments, suggestions or
successful experiences in the forum of http://www.CLooG.org
or to send them to cedric.bastoul@inria.fr directly.
If you want to use CLooG, this is because you want to scan or to find something inside the integral points of a set of polyhedra. There are many reasons for that. Maybe you need the generated code itself because it actually implements a very smart program transformation you found. Maybe you want to use the generated code because you know that the solution of your problem belongs to the integral points of those damned polyhedra and you don't know which one. Maybe you just want to know if a polyhedron has integral points depending on some parameters, which is the lexicographic minimum, maximum, the third on the basis of the left etc. Probably you have your own reasons to use CLooG.
Let us illustrate a basic use of CLooG. Suppose we have a set of affine constraints that describes a part of a whatever-dimensional space, called a domain, and we want to scan it. Let us consider for instance the following set of constraints where `i' and `j' are the unknown (the two dimensions of the space) and `m' and `n' are the parameters (some symbolic constants):
2<=i<=n
2<=j<=m
j<=n+2-i
Let us also consider that we have a partial knowledge of the parameter values, called the context, expressed as affine constraints as well, for instance:
m>=2
n>=2
Note that using parameters is optional, if you are not comfortable with
parameter manipulation, just replace them with any scalar value that fits
m>=2 and n>=2.
A graphical representation of this part of the 2-dimensional space, where
the integral points are represented using heavy dots would be for instance:
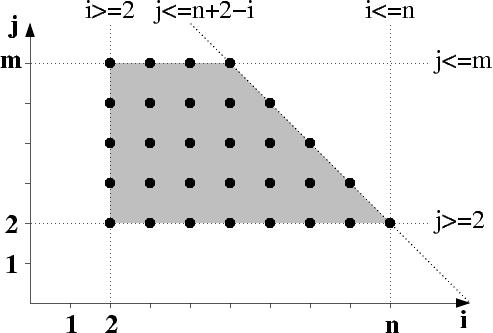
The affine constraints of both the domain and the context are what we will provide to CLooG as input (in a particular shape that will be described later). The output of CLooG is a pseudo-code to scan the integral points of the input domain according to the context:
for (i=2;i<=n;i++) {
for (j=2;j<=min(m,-i+n+2);j++) {
S1(i,j) ;
}
}
If you felt such a basic example is yet interesting, there is a good chance that CLooG is appropriate for you. CLooG can do much more: scanning several polyhedra or unions of polyhedra at the same time, applying general affine transformations to the polyhedra, generate compilable code etc. Welcome to the CLooG's user's guide !
In CLooG, domains only define the set of integral points to scan and their
coordinates. In particular, CLooG is free to choose the scanning order for
generating the most efficient code. This means, for optimizing/parallelizing
compiler people, that CLooG doesn't make any speculation on dependences on and
between statements (by the way, it's not its job !).
For instance, if an user give to
CLooG only two domains S1:1<=i<=n, S2:1<=i<=n and the context
n>=1, the following pseudo-codes are considered to be equivalent:
/* A convenient target pseudo-code. */
for (i=1;i<=N;i++) {
S1(i) ;
}
for (i=1;i<=N;i++) {
S2(i) ;
}
/* Another convenient target pseudo-code. */
for (i=1;i<=N;i++) {
S1(i) ;
S2(i) ;
}
The default behaviour
of CLooG is to generate the second one, since it is optimized in control.
It is right if there are no data dependences
between S1 and S2, but wrong otherwise.
Thus it is often useful to force scanning to respect a given order. This can be done in CLooG by using scattering functions. Scattering is a shortcut for scheduling, allocation, chunking functions and the like we can find in the restructuring compilation literature. There are a lot of reasons to scatter the integral points of the domains (i.e. the statement instances of a program, for compilation people), parallelization or optimization are good examples. For instance, if the user wants for any reason to set some precedence constraints between the statements of our example above in order to force the generation of the first code, he can do it easily by setting (for example) the following scheduling functions:
T_S1(i) = (1)
T_S2(j) = (2)
This scattering means that each integral point of the domain S1
is scanned at logical date 1 while each integral point of the domain
S2 is scanned at logical date 2. As a result, the whole
domain S1 is scanned before domain S2 and the first code in our
example is generated.
The user can set every kind of affine scanning order thanks to the
scattering functions. Each domain has its own scattering function and
each scattering function may be multi-dimensional. A multi-dimensional logical
date may be seen as classical date (year,month,day,hour,minute,etc.) where
the first dimensions are the most significant. Each scattering dimension
may depend linearly on the original dimensions (e.g., i), the
parameters (e.g., n) ans scalars (e.g., 2).
A very useful example of multi-dimensional scattering functions is, for compilation people, the scheduling of the original program. The basic data to use for code generation are statement iteration domains. As we saw, these data are not sufficient to rebuild the original program (what is the ordering between instances of different statements ?). The missing data can be put in the scattering functions as the original scheduling. The method to compute it is quite simple (see Fea92). The idea is to build an abstract syntax tree of the program and to read the scheduling for each statement. For instance, let us consider the following implementation of a Cholesky factorization:
/* A Cholesky factorization kernel. */
for (i=1;i<=N;i++) {
for (j=1;j<=i-1;j++) {
a[i][i] -= a[i][j] ; /* S1 */
}
a[i][i] = sqrt(a[i][i]) ; /* S2 */
for (j=i+1;j<=N;j++) {
for (k=1;k<=i-1;k++) {
a[j][i] -= a[j][k]*a[i][k] ; /* S3 */
}
a[j][i] /= a[i][i] ; /* S4 */
}
}
}
The corresponding abstract syntax tree is given in the following figure. It directly gives the scattering functions (schedules) for all the statements of the program.
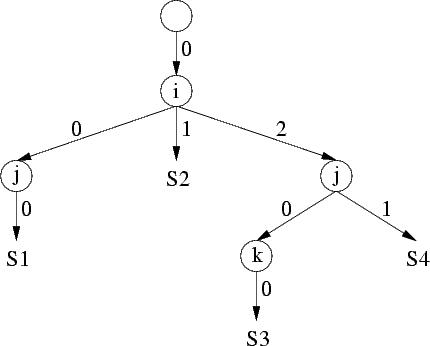
T_S1(i,j)^T = (0,i,0,j,0)^T
T_S2(i) = (0,i,1)^T
T_S3(i,j,k)^T = (0,i,2,j,0,k,0)^T
T_S4(i,j)^T = (0,i,2,j,1)^T
These schedules depend on the iterators and give for each instance of each statement a unique execution date. Using such scattering functions allow CLooG to re-generate the input code.
CLooG takes as input a file that must be written accordingly to a grammar described in depth in a further section (see Writing The Input File). Moreover it supports many options to tune the target code presentation or quality as discussed in a dedicated section (see Calling CLooG). However, a basic use of CLooG is not very complex and we present in this section how to generate the code corresponding to a basic example discussed earlier (see Basics).
The problem is to find the code that scans a 2-dimensional polyhedron where `i' and `j' are the unknown (the two dimensions of the space) and `m' and `n' are the parameters (the symbolic constants), defined by the following set of constraints:
2<=i<=n
2<=j<=m
j<=n+2-i
We also consider a partial knowledge of the parameter values, expressed thanks to the following affine constraints:
m>=2
n>=2
An input file that corresponds to this problem, and asks for a generated code in C, may be the following. Note that we do not describe here precisely the structure and the components of this file (see Writing The Input File for such information, if you feel it necessary):
# ---------------------- CONTEXT ----------------------
c # language is C
# Context (constraints on two parameters)
2 4 # 2 lines and 4 columns
# eq/in m n 1 eq/in: 1 for inequality >=0, 0 for equality =0
1 1 0 -2 # 1*m + 0*n -2*1 >= 0, i.e. m>=2
1 0 1 -2 # 0*m + 1*n -2*1 >= 0, i.e. n>=2
1 # We want to set manually the parameter names
m n # parameter names
# --------------------- STATEMENTS --------------------
1 # Number of statements
1 # First statement: one domain
# First domain
5 6 # 5 lines and 6 columns
# eq/in i j m n 1
1 1 0 0 0 -2 # i >= 2
1 -1 0 0 1 0 # i <= n
1 0 1 0 0 -2 # j >= 2
1 0 -1 1 0 0 # j <= m
1 -1 -1 0 1 2 # n+2-i>=j
0 0 0 # for future options
1 # We want to set manually the iterator names
i j # iterator names
# --------------------- SCATTERING --------------------
0 # No scattering functions
This file may be called `basic.cloog'
(this example is provided in the CLooG distribution as
test/manual_basic.cloog) and we can ask CLooG to process it
and to generate the code by a simple calling to CLooG with this file as input:
`cloog basic.cloog'. By default, CLooG will print the generated code in
the standard output:
/* Generated by CLooG v{No value for `VERSION'} in 0.00s. */
for (i=2;i<=n;i++) {
for (j=2;j<=min(m,-i+n+2);j++) {
S1(i,j) ;
}
}
The input text file contains a problem description, i.e. the context, the domains and the scattering functions. Because CLooG is very 'compilable code generation oriented', we can associate some additional informations to each domain. We call this association a statement. The set of all informations is called a program. The input file respects the grammar below (terminals are preceded by "_"):
File ::= Program
Program ::= Context Statements Scattering
Context ::= Language Domain_union Naming
Statements ::= Nb_statements Statement_list Naming
Scatterings ::= Nb_functions Scattering_list Naming
Naming ::= Option Name_list
Name_list ::= _String Name_list | (void)
Statement_list ::= Statement Statement_list | (void)
Domain_list ::= _Domain Domain_list | (void)
Scattering_list ::= Domain_union Scattering_list | (void)
Statement ::= Iteration_domain 0 0 0
Iteration_domain ::= Domain_union
Domain_union ::= Nb_domains Domain_list
Option ::= 0 | 1
Language ::= c | f
Nb_statements ::= _Integer
Nb_domains ::= _Integer
Nb_functions ::= _Integer
Note: if there is only one domain in a `Domain_union', i.e., if `Nb_domains' is 1, then this 1 may be omitted.
As shown by the grammar, the input file describes the various informations thanks to characters, integers and domains. Each domain is defined by a set of constraints in the PolyLib format (see Wil93). They have the following syntax:
-i + m >= 0
-j + n >= 0
i + j - k >= 0
can be written in the input file as follows :
# This is the domain
3 7 # 3 lines and 7 columns
# eq/in i j k m n 1
1 -1 0 0 1 0 0 # -i + m >= 0
1 0 -1 0 0 1 0 # -j + n >= 0
1 1 1 -1 0 0 0 # i + j - k >= 0
Each iteration domain `Iteration_domain' of a given statement is a union of polyhedra `Domain_union'. A union is defined by its number of elements `Nb_domains' and the elements themselves `Domain_list'. For instance, let us consider the following pseudo-code:
for (i=1;i<=n;i++) {
if ((i >= m) || (i <= 2*m))
S1 ;
for (j=i+1;j<=m;j++)
S2 ;
}
The iteration domain of `S1' can be divided into two polyhedra and written in the input file as follows:
2 # Number of polyhedra in the union
# First domain
3 5 # 3 lines and 5 columns
# eq/in i m n 1
1 1 0 0 -1 # i >= 1
1 -1 0 1 0 # i <= n
1 1 -1 0 0 # i >= m
# Second domain
3 5 # 3 lines and 5 columns
# eq/in i m n 1
1 1 0 0 -1 # i >= 1
1 -1 0 1 0 # i <= n
1 -1 2 0 0 # i <= 2*m
Scattering functions are depicted in the input file thanks a representation very close to the domain one. An integer gives the number of functions `Nb_functions' and each function is represented by a domain. Each line of the domain corresponds to an equality defining a dimension of the function. Note that at present (CLooG {No value for `VERSION'}) all functions must have the same scattering dimension number. If a user wants to set scattering functions with different dimensionality, he has to complete the smaller one with zeroes to reach the maximum dimensionality. For instance, let us consider the following code and scheduling functions:
for (i=1;i<=n;i++) {
if ((i >= m) || (i <= 2*m))
S1 ;
for (j=i+1;j<=m;j++)
S2 ;
}
T_S1(i) = (i,0)^T
T_S2(i,j)^T = (n,i+j)^T
This scheduling can be written in the input file as follows:
2 # Number of scattering functions
# First function
2 7 # 2 lines and 7 columns
# eq/in c1 c2 i m n 1
0 1 0 -1 0 0 0 # c1 = i
0 0 1 0 0 0 0 # c2 = 0
# Second function
2 8 # 2 lines and 8 columns
# eq/in c1 c2 i j m n 1
0 1 0 0 0 0 -1 0 # c1 = n
0 0 1 -1 -1 0 0 0 # c2 = i+j
The complete input file for the user who wants to generate the code for this
example with the preceding scheduling would be
(this file is provided in the CLooG distribution
as test/manual_scattering.cloog:
# ---------------------- CONTEXT ----------------------
c # language is C
# Context (no constraints on two parameters)
1 4 # 1 lines and 4 columns
# eq/in m n 1
1 0 0 0 # 0 >= 0, always true
1 # We want to set manually the parameter names
m n # parameter names
# --------------------- STATEMENTS --------------------
2 # Number of statements
2 # First statement: two domains
# First domain
3 5 # 3 lines and 5 columns
# eq/in i m n 1
1 1 0 0 -1 # i >= 1
1 -1 0 1 0 # i <= n
1 1 -1 0 0 # i >= m
# Second domain
3 5 # 3 lines and 5 columns
# eq/in i m n 1
1 1 0 0 -1 # i >= 1
1 -1 0 1 0 # i <= n
1 -1 2 0 0 # i <= 2*m
0 0 0 # for future options
1 # Second statement: one domain
4 6 # 4 lines and 6 columns
# eq/in i j m n 1
1 1 0 0 0 -1 # i >= 1
1 -1 0 0 1 0 # i <= n
1 -1 1 0 0 -1 # j >= i+1
1 0 -1 1 0 0 # j <= m
0 0 0 # for future options
1 # We want to set manually the iterator names
i j # iterator names
# --------------------- SCATTERING --------------------
2 # Scattering functions
# First function
2 7 # 2 lines and 7 columns
# eq/in p1 p2 i m n 1
0 1 0 -1 0 0 0 # p1 = i
0 0 1 0 0 0 0 # p2 = 0
# Second function
2 8 # 2 lines and 8 columns
# eq/in p1 p2 i j m n 1
0 1 0 0 0 0 -1 0 # p1 = n
0 0 1 -1 -1 0 0 0 # p2 = i+j
1 # We want to set manually the scattering dimension names
p1 p2 # scattering dimension names
CLooG is called by the following command:
cloog [ options | file ]
The default behavior of CLooG is to read the input informations from a file and
to print the generated code or pseudo-code on the standard output.
CLooG's behavior and the output code shape is under the user control thanks
to many options which are detailed a further section (see CLooG Options).
file is the input file. stdin is a special value: when used,
input is standard input. For instance, we can call CLooG to treat the
input file basic.cloog with default options by typing:
cloog basic.cloog or more basic.cloog | cloog stdin.
-l <depth>-l <depth>: this option sets the last loop depth to be optimized in
control. The higher this depth, the less control overhead.
For instance, with some input file, a user can generate
different pseudo-codes with different depth values as shown below.
/* Generated using a given input file and option -l 1 */
for (i=0;i<=M;i++) {
S1 ;
for (j=0;j<=N;j++) {
S2 ;
}
for (j=0;j<=N;j++) {
S3 ;
}
S4 ;
}
/* Generated using the same input file but option -l 2 */
for (i=0;i<=M;i++) {
S1 ;
for (j=0;j<=N;j++) {
S2 ;
S3 ;
}
S4 ;
}
In this example we can see that this option can change the operation
execution order between statements. Let us remind that CLooG does not
make any speculation on dependences between statements
(see Scattering). Thus if nothing (i.e. scattering functions)
forbids this, CLooG considers the above codes to be equivalent.
If there is no scattering functions, the minimum value for depth
is 1 (in the case of 0, the user doesn't really need a loop generator !),
and the number of scattering dimensions otherwise (CLooG will warn the
user if he doesn't respect such constraint).
The maximum value for depth is -1 (infinity).
Default value is infinity.
-f <depth>-f <depth>: this option sets the first loop depth to be optimized
in control. The lower this depth, the less control overhead (and the longer
the generated code). For instance, with some input file, a user
can generate different pseudo-codes with different depth values
as shown below.
The minimum value for depth is 1, and the
maximum value is -1 (infinity).
Default value is 1.
/* Generated using a given input file and option -f 3 */
for (i=1;i<=N;i++) {
for (j=1;j<=M;j++) {
S1 ;
if (j >= 10) {
S2 ;
}
}
}
/* Generated using the same input file but option -f 2 */
for (i=1;i<=N;i++) {
for (j=1;j<=9;j++) {
S1 ;
}
for (j=10;j<=M;j++) {
S1 ;
S2 ;
}
}
-sh <boolean>-sh <boolean>: this option enables (boolean=1)
or forbids (boolean=0) a simplification step
that may simplify some constraints.
This option works only for generated code without
code duplication (it means, you have to tune -f and
-l options first to generate only a loop nest with internal
guards). For instance, with the input file test/union.cloog, a user
can generate different pseudo-codes as shown below.
Default value is 0.
/* Generated using test/union.cloog and option -f -1 -l 2 -override */
for (i=0;i<=11;i++) {
for (j=max(0,5*i-50);j<=min(15,5*i+10);j++) {
if ((i <= 10) && (j <= 10)) {
S1 ;
}
if ((i >= 1) && (j >= 5)) {
S2 ;
}
}
}
/* Generated using the same input file but option -sh 1 -f -1 -l 2 -override */
for (i=0;i<=11;i++) {
for (j=0;j<=15;j++) {
if ((i <= 10) && (j <= 10)) {
S1 ;
}
if ((i >= 1) && (j >= 5)) {
S2 ;
}
}
}
-otl <boolean>-otl <boolean>: this option allows (boolean=1) or
forbids (boolean=0) the simplification of loops running
once. Default value is 1.
/* Generated using a given input file and option -otl 0 */
for (j=i+1;j<=i+1;j++) {
S1 ;
}
/* Generated using the same input file but option -otl 1 */
j = i+1 ;
S1 ;
-esp <boolean>-esp <boolean>: this option allows (boolean=1) or
forbids (boolean=0) values spreading when there
are equalities. Default value is 1.
/* Generated using a given input file and option -esp 0 */
i = M+2 ;
j = N ;
for (k=i;k<=j+M;k++) {
S1 ;
}
/* Generated using the same input file but option -esp 1 */
for (k=M+2;k<=N+M;k++) {
S1(i = M+2, j = N) ;
}
-fsp <level>-fsp <level>: it can be useful to set a
first level to begin equality spreading. Particularly when using
scattering functions, the user may want to see the scattering dimension
values instead of spreading or hiding them. If user has set a
spreading, level is
the first level to start it. Default value is 1.
/* Generated using a given input file and option -fsp 1 */
for (j=0;j<=N+M;j++) {
S1(i = N) ;
}
for (j=0;j<=N+M;j++) {
S1(i = M) ;
}
/* Generated using the same input file but option -fsp 2 */
c1 = N ;
for (j=0;j<=c1+M;j++) {
S1(i = c1) ;
}
c1 = M ;
for (j=0;j<=N+c1;j++) {
S1(i = c1) ;
}
-block <boolean>-block <boolean>: this option allows (boolean=1) to
create a statement block for each new iterator, even if there is only
an equality. This can be useful in order to parse the generated
pseudo-code. When boolean is set to 0 or when the generation
language is FORTRAN, this feature is disabled. Default value is 0.
/* Generated using a given input file and option -block 0 */
i = M+2 ;
j = N ;
S1 ;
/* Generated using the same input file but option -block 1 */
{ i = M+2 ;
{ j = N ;
S1 ;
}
}
-strides <boolean>-strides <boolean>: this options allows (boolean=1) to
handle non-unit strides for loop increments. This can remove a lot of
guards and make the generated code more efficient. Default value is 0.
/* Generated using a given input file and option -strides 0 */
for (i=1;i<=n;i++) {
if (i%2 == 0) {
S1(j = i/2) ;
}
if (i%4 == 0) {
S2(j = i/4) ;
}
}
/* Generated using the same input file but option -strides 1 */
for (i=2;i<=n;i+=2) {
S1(j = i/2) ;
if (i%4 == 0) {
S2(j = i/4) ;
}
}
-compilable <value>-compilable <value>: this options allows (value is not 0)
to generate a compilable code where all parameters have the integral value
value. This option creates a macro for each statement. Since
CLooG do not know anything about the statement sources, it fills the
macros with a basic increment that computes the total number of
scanned integral points. The user may change easily the macros according
to his own needs. This option is possible only if the generated code is
in C. Default value is 0.
/* Generated using a given input file and option -compilable 0 */
for (i=0;i<=n;i++) {
for (j=0;j<=n;j++) {
S1 ;
S2 ;
}
S3 ;
}
/* Generated using the same input file but option -compilable 10 */
/* DON'T FORGET TO USE -lm OPTION TO COMPILE. */
/* Useful headers. */
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
/* Parameter value. */
#define PARVAL 10
/* Statement macros (please set). */
#define S1(i,j) {total++;}
#define S2(i,j) {total++;}
#define S3(i) {total++;}
int main() {
/* Original iterators. */
int i, j ;
/* Parameters. */
int n=PARVAL, total=0 ;
for (i=0;i<=n;i++) {
for (j=0;j<=n;j++) {
S1(i,j) ;
S2(i,j) ;
}
S3(i) ;
}
printf("Number of integral points: %d.\n",total) ;
return 0 ;
}
-callable <boolean>-callable <boolean>: if boolean=1, then a test
function will be generated that has the parameters as arguments.
Similarly to the -compilable option,
a macro for each statement is generated. The generated definitions of
these macros are as used during the correctness testing, but they
can easily be changed by the user to suit her own needs.
This option is only available if the target language is C.
The default value is 0.
/* Generated from double.cloog with option -callable 0 */
for (i=0;i<=M;i++) {
S1 ;
for (j=0;j<=N;j++) {
S2 ;
S3 ;
}
S4 ;
}
/* Generated from double.cloog with option -callable 1 */
extern void hash(int);
/* Useful macros. */
#define floord(n,d) (((n)<0) ? ((n)-(d)+1)/(d) : (n)/(d))
#define ceild(n,d) (((n)<0) ? (n)/(d) : ((n)+(d)+1)/(d))
#define max(x,y) ((x) > (y) ? (x) : (y))
#define min(x,y) ((x) < (y) ? (x) : (y))
#define S1(i) { hash(1); hash(i); }
#define S2(i,j) { hash(2); hash(i); hash(j); }
#define S3(i,j) { hash(3); hash(i); hash(j); }
#define S4(i) { hash(4); hash(i); }
void test(int M, int N)
{
/* Original iterators. */
int i, j;
for (i=0;i<=M;i++) {
S1(i) ;
for (j=0;j<=N;j++) {
S2(i,j) ;
S3(i,j) ;
}
S4(i) ;
}
}
-o <output>-o <output>: this option sets the output file. stdout is a
special value: when used, output is standard output.
Default value is stdout.
--help or -h--help or -h: this option ask CLooG to print a short help.
--version or -v--version or -v: this option ask CLooG to print some version
informations.
--quiet or -q--quiet or -q: this option tells CLooG not to print
any informational messages.
Let us consider the allocation problem of a Gaussian elimination, i.e. we want to distribute the various statement instances of the compute kernel onto different processors. The original code is the following:
for (i=1;j<=N-1;i++) {
for (j=i+1;j<=N;j++) {
c[i][j] = a[j][i]/a[i][i] ; /* S1 */
for (k=i+1;k<=N;k++) {
a[j][k] -= c[i][j]*a[i][k] ; /* S2 */
}
}
}
The best affine allocation functions can be found by any good automatic parallelizer like LooPo (see Gri04):
T_S1(i,j)^T = (i)
T_S2(i,j,k)^T = (k)
To ensure that on each processor, the set of statement instances is executed according to the original ordering, we add as minor scattering dimensions the original scheduling (see Scattering):
T_S1(i,j)^T = (i,0,i,0,j,0)^T
T_S2(i,j,k)^T = (k,0,i,0,j,1,k,0)^T
To ensure that the scattering functions have the same dimensionality, we complete the first function with zeroes (this is a CLooG {No value for `VERSION'} and previous versions requirement, it should be removed in a future version, don't worry it's absolutely legal !):
T_S1(i,j)^T = (i,0,i,0,j,0,0,0)^T
T_S2(i,j,k)^T = (k,0,i,0,j,1,k,0)^T
The input file corresponding to this code generation problem
could be (this file is provided in the CLooG distribution
as test/manual_gauss.cloog:
# ---------------------- CONTEXT ----------------------
c # language is C
# Context (no constraints on one parameter)
1 3 # 1 line and 3 columns
# eq/in n 1
1 0 0 # 0 >= 0, always true
1 # We want to set manually the parameter name
n # parameter name
# --------------------- STATEMENTS --------------------
2 # Number of statements
1 # First statement: one domain
4 5 # 4 lines and 3 columns
# eq/in i j n 1
1 1 0 0 -1 # i >= 1
1 -1 0 1 -1 # i <= n-1
1 -1 1 0 -1 # j >= i+1
1 0 -1 1 0 # j <= n
0 0 0 # for future options
1
# Second statement: one domain
6 6 # 6 lines and 3 columns
# eq/in i j k n 1
1 1 0 0 0 -1 # i >= 1
1 -1 0 0 1 -1 # i <= n-1
1 -1 1 0 0 -1 # j >= i+1
1 0 -1 0 1 0 # j <= n
1 -1 0 1 0 -1 # k >= i+1
1 0 0 -1 1 0 # k <= n
0 0 0 # for future options
0 # We let CLooG set the iterator names
# --------------------- SCATTERING --------------------
2 # Scattering functions
# First function
8 13 # 3 lines and 3 columns
# eq/in p1 p2 p3 p4 p5 p6 p7 p8 i j n 1
0 1 0 0 0 0 0 0 0 -1 0 0 0 # p1 = i
0 0 1 0 0 0 0 0 0 0 0 0 0 # p2 = 0
0 0 0 1 0 0 0 0 0 -1 0 0 0 # p3 = i
0 0 0 0 1 0 0 0 0 0 0 0 0 # p4 = 0
0 0 0 0 0 1 0 0 0 0 -1 0 0 # p5 = j
0 0 0 0 0 0 1 0 0 0 0 0 0 # p6 = 0
0 0 0 0 0 0 0 1 0 0 0 0 0 # p7 = 0
0 0 0 0 0 0 0 0 1 0 0 0 0 # p8 = 0
# Second function
8 14 # 3 lines and 3 columns
# eq/in p1 p2 p3 p4 p5 p6 p7 p8 i j k n 1
0 1 0 0 0 0 0 0 0 0 0 -1 0 0 # p1 = k
0 0 1 0 0 0 0 0 0 0 0 0 0 0 # p2 = 0
0 0 0 1 0 0 0 0 0 -1 0 0 0 0 # p3 = i
0 0 0 0 1 0 0 0 0 0 0 0 0 0 # p4 = 0
0 0 0 0 0 1 0 0 0 0 -1 0 0 0 # p5 = j
0 0 0 0 0 0 1 0 0 0 0 0 0 -1 # p6 = 1
0 0 0 0 0 0 0 1 0 0 0 -1 0 0 # p7 = k
0 0 0 0 0 0 0 0 1 0 0 0 0 0 # p8 = 0
1 # We want to set manually the scattering dimension names
p1 p2 p3 p4 p5 p6 p7 p8 # scattering dimension names
Calling CLooG, with for instance the command line
cloog -fsp 2 gauss.cloog for a better view
of the allocation (the processor number is given by p1),
will result on the following target code that actually implements
the transformation. A minor processing on the dimension p1
to implement, e.g., MPI calls, which is not shown here may
result in dramatic speedups !
if (n >= 2) {
p1 = 1 ;
for (p5=2;p5<=n;p5++) {
S1(i = 1,j = p5) ;
}
}
for (p1=2;p1<=n-1;p1++) {
for (p3=1;p3<=p1-1;p3++) {
for (p5=p3+1;p5<=n;p5++) {
S2(i = p3,j = p5,k = p1) ;
}
}
for (p5=p1+1;p5<=n;p5++) {
S1(i = p1,j = p5) ;
}
}
if (n >= 2) {
p1 = n ;
for (p3=1;p3<=n-1;p3++) {
for (p5=p3+1;p5<=n;p5++) {
S2(i = p3,j = p5,k = n) ;
}
}
}
The CLooG Library was implemented to allow the user to call CLooG
directly from his programs, without file accesses or system calls. The
user only needs to link his programs with C libraries. The CLooG
library mainly provides one function (cloog_clast_create_from_input)
which takes as input the problem
description with some options, and returns the data structure corresponding
to the generated code (a struct clast_stmt structure)
which is more or less an abstract syntax tree.
The user can work with this data structure and/or use
our pretty printing function to write the final code in either C or FORTRAN.
Some other functions are provided for convenience reasons.
These functions as well as the data structures are described in this section.
In this section, we describe the data structures used by the loop generator to represent and to process a code generation problem.
CloogState *cloog_state_malloc(void);
void cloog_state_free(CloogState *state);
The CloogState structure is (implicitly) needed to perform
any CLooG operation. It should be created using cloog_state_malloc
before any other CLooG objects are created and destroyed using
cloog_state_free after all objects have been freed.
It is allowed to use more than one CloogState structure at
the same time, but an object created within the state of a one
CloogState structure is not allowed to interact with an object
created within the state of an other CloogState structure.
The CloogMatrix structure is equivalent to the PolyLib
Matrix data structure (see Wil93). This structure is devoted to
represent a set of constraints.
struct cloogmatrix
{ unsigned NbRows ; /* Number of rows. */
unsigned NbColumns ; /* Number of columns. */
cloog_int_t **p; /* Array of pointers to the matrix rows. */
cloog_int_t *p_Init; /* Matrix rows contiguously in memory. */
};
typedef struct cloogmatrix CloogMatrix;
CloogMatrix *cloog_matrix_alloc(unsigned NbRows, unsigned NbColumns);
void cloog_matrix_print(FILE *foo, CloogMatrix *m);
void cloog_matrix_free(CloogMatrix *matrix);
The whole matrix is stored in memory row after row at the
p_Init address. p is an array of pointers where
p[i] points to the first element of the i^th row.
NbRows and NbColumns are respectively the number of
rows and columns of the matrix.
Each row corresponds to a constraint. The first element of each row is an
equality/inequality tag. The
constraint is an equality p(x) = 0 if the first element is 0, but it is
an inequality p(x) \geq 0 if the first element is 1.
The next elements are the coefficients of the unknowns,
followed by the coefficients of the parameters, and finally the constant term.
For instance, the following three constraints:
-i + m = 0
-j + n >= 0
i + j - k >= 0
would be represented by the following rows:
# eq/in i j k m n cst
0 0 -1 0 1 0 0
1 -1 0 0 0 1 0
1 1 1 -1 0 0 0
To be able to provide different precision version (CLooG
supports 32 bits, 64 bits and arbitrary precision through the GMP library),
the cloog_int_t type depends on the configuration options (it may be
long int for 32 bits version, long long int for 64 bits version,
and mpz_t for multiple precision version).
CloogDomain *cloog_domain_union_read(CloogState *state,
FILE *input, int nb_parameters);
CloogDomain *cloog_domain_from_cloog_matrix(CloogState *state,
CloogMatrix *matrix, int nb_par);
void cloog_domain_free(CloogDomain *domain);
CloogDomain is an opaque type representing a polyhedral
domain (a union of polyhedra).
A CloogDomain can be read
from a file using cloog_domain_union_read or
converted from a CloogMatrix.
The input format for cloog_domain_union_read
is that of Domain Representation.
The function cloog_domain_from_cloog_matrix takes a CloogState, a
CloogMatrix and int as input and returns a pointer to a
CloogDomain. matrix describes the domain and nb_par is the
number of parameters in this domain. The input data structures are neither
modified nor freed.
The CloogDomain can be freed using cloog_domain_free.
There are also some backend dependent functions for creating
CloogDomains.
#include <cloog/polylib/cloog.h>
CloogDomain *cloog_domain_from_polylib_polyhedron(CloogState *state,
Polyhedron *, int nb_par);
The function cloog_domain_from_polylib_polyhedron takes a PolyLib
Polyhedron as input and returns a pointer to a CloogDomain.
The nb_par parameter indicates the number of parameters
in the domain. The input data structure if neither modified nor freed.
#include <cloog/isl/cloog.h>
CloogDomain *cloog_domain_from_isl_set(struct isl_set *set);
__isl_give isl_set *isl_set_from_cloog_domain(CloogDomain *domain);
The function cloog_domain_from_isl_set takes a
struct isl_set as input and returns a pointer to a CloogDomain.
The function consumes a reference to the given struct isl_set.
Similarly, isl_set_from_cloog_domain consumes a reference
to a CloogDomain and returns an isl_set.
CloogScattering *cloog_domain_read_scattering(CloogDomain *domain,
FILE *foo);
CloogScattering *cloog_scattering_from_cloog_matrix(CloogState *state,
CloogMatrix *matrix, int nb_scat, int nb_par);
void cloog_scattering_free(CloogScattering *);
The CloogScattering type represents a scattering function.
A CloogScattering for a given CloogDomain can be read
from a file using cloog_scattering_read or converted
from a CloogMatrix using cloog_scattering_from_cloog_matrix.
The function cloog_scattering_from_cloog_matrix takes a
CloogState, a CloogMatrix and two ints as input and
returns a
pointer to a CloogScattering.
matrix describes the scattering, while nb_scat and
nb_par are the number of scattering dimensions and
the number of parameters, respectively. The input data structures are
neither modified nor freed.
A CloogScattering can be freed using cloog_scattering_free.
There are also some backend dependent functions for creating
CloogScatterings.
#include <cloog/polylib/cloog.h>
CloogScattering *cloog_scattering_from_polylib_polyhedron(
CloogState *state, Polyhedron *polyhedron, int nb_par);
The function cloog_scattering_from_polylib_polyhedron takes a PolyLib
Polyhedron as input and returns a pointer to a CloogScattering.
The nb_par parameter indicates the number of parameters
in the domain. The input data structure if neither modified nor freed.
#include <cloog/isl/cloog.h>
CloogScattering *cloog_scattering_from_isl_map(struct isl_map *map);
The function cloog_scattering_from_isl_map takes a
struct isl_map as input and returns a pointer to a CloogScattering.
The output dimensions of the struct isl_map correspond to the
scattering dimensions, while the input dimensions correspond to the
domain dimensions.
The function consumes a reference to the given struct isl_map.
enum cloog_dim_type { CLOOG_PARAM, CLOOG_ITER, CLOOG_SCAT };
CloogUnionDomain *cloog_union_domain_alloc(int nb_par);
CloogUnionDomain *cloog_union_domain_add_domain(CloogUnionDomain *ud,
const char *name, CloogDomain *domain,
CloogScattering *scattering, void *usr);
CloogUnionDomain *cloog_union_domain_set_name(CloogUnionDomain *ud,
enum cloog_dim_type type, int index, const char *name);
void cloog_union_domain_free(CloogUnionDomain *ud);
A CloogUnionDomain structure represents a union
of scattered named domains. A CloogUnionDomain is
initialized by a call to cloog_union_domain_alloc,
after which domains can be added using cloog_union_domain_add_domain.
cloog_union_domain_alloc takes the number of parameters as input.
cloog_union_domain_add_domain takes a previously created
CloogUnionDomain as input along with an optional name,
a domain, an optional scattering function and a user pointer.
The name may be NULL and is duplicated if it is not.
If no name is specified, then the statements will be named according
to the order in which they were added.
domain and scattering are taken over
by the CloogUnionDomain. scattering may be NULL,
but it must be consistently NULL or not over all calls
to cloog_union_domain_add_domain.
cloog_union_domain_set_name can be used to set the names
of parameters, iterators and scattering dimensions.
The names of iterators and scattering dimensions can only be set
after all domains have been added.
There is also a backend dependent function for creating
CloogUnionDomains.
#include <cloog/isl/cloog.h>
CloogUnionDomain *cloog_union_domain_from_isl_union_map(
__isl_take isl_union_map *umap);
CloogUnionDomain *cloog_union_domain_from_isl_union_set(
__isl_take isl_union_set *uset);
The function cloog_union_domain_from_isl_union_map takes a
isl_union_map as input and returns a pointer
to a CloogUnionDomain.
The input is a mapping from different
spaces (different tuple names and possibly different dimensions)
to a common space. The iteration domains are set to the domains
in each space. The statement names are set to the names of the
spaces. The parameter names of the result are set to those of
the input, but the iterator and scattering dimension names are
left unspecified.
The function consumes a reference to the given isl_union_map.
The function cloog_union_domain_from_isl_union_set is similar,
but takes unscattered domains as input.
struct cloogstatement
{ int number ; /* The statement unique number. */
char *name; /* Name of the statement. */
void * usr ; /* Pointer for user's convenience. */
struct cloogstatement * next ;/* Next element of the linked list. */
} ;
typedef struct cloogstatement CloogStatement ;
CloogStatement *cloog_statement_malloc(CloogState *state);
void cloog_statement_print(FILE *, CloogStatement *);
void cloog_statement_free(CloogStatement *);
The CloogStatement structure represents a NULL
terminated linked
list of statements. In CLooG, a statement is only defined by its unique
number (number). The user can use the pointer usr for his
own convenience to link his own statement representation to the
corresponding CloogStatement structure. The whole management of the
usr pointer is under the responsibility of the user, in particular,
CLooG never tries to print, to allocate or to free a memory block pointed
by usr.
struct cloogoptions
{ int l ; /* -l option. */
int f ; /* -f option. */
int strides ; /* -strides option. */
int sh ; /* -sh option. */
int esp ; /* -esp option. */
int fsp ; /* -fsp option. */
int otl ; /* -otl option. */
int block ; /* -block option. */
int cpp ; /* -cpp option. */
int compilable ; /* -compilable option. */
int language; /* LANGUAGE_C or LANGUAGE_FORTRAN */
int save_domains; /* Save unsimplified copy of domain. */
} ;
typedef struct cloogoptions CloogOptions ;
CloogOptions *cloog_options_malloc(CloogState *state);
void cloog_options_print(FILE *foo, CloogOptions *options);
void cloog_options_free(CloogOptions *options);
The CloogOptions structure contains all the possible options to
rule CLooG's behaviour (see Calling CLooG).
As a reminder, the default values are:
The save_domains option is only useful for users of the CLooG
library. This option defaults to 0, but when it is set, the domain
field of each clast_user_stmt will be set to the set of values for the
scattering dimensions for which this instance of the user statement is executed.
The domain field of each clast_for contains the set of values for
the scattering dimensions for which an instance of a user statement is executed
inside the clast_for. It is only available if the clast_for
enumerates a scattering dimension.
CloogInput *cloog_input_read(FILE *file, CloogOptions *options);
CloogInput *cloog_input_alloc(CloogDomain *context,
CloogUnionDomain *ud);
void cloog_input_free(CloogInput *input);
void cloog_input_dump_cloog(FILE *, CloogInput *, CloogOptions *);
A CloogInput structure represents the input to CLooG.
It is essentially a CloogUnionDomain along with a context
CloogDomain. A CloogInput can be created from
a CloogDomain and a CloogUnionDomains using
cloog_input_alloc, or it can be read from a CLooG input
file using cloog_input_read. The latter also modifies
the language field of the CloogOptions structure.
The constructed CloogInput can be used as input
to a cloog_clast_create_from_input call.
A CloogInput data structure and a CloogOptions contain
the same information as a .cloog file. This function dumps the .cloog
description of the given data structures into a file.
Given a description of the input,
an AST corresponding to the CloogInput can be constructed
using cloog_clast_create_from_input and destroyed using
free_clast_stmt.
struct clast_stmt *cloog_clast_create_from_input(CloogInput *input,
CloogOptions *options);
void free_clast_stmt(struct clast_stmt *s);
clast_stmt represents a linked list of “statements”.
struct clast_stmt {
const struct clast_stmt_op *op;
struct clast_stmt *next;
};
The entries in the list are not of type clast_stmt itself,
but of some larger type. The following statement types are defined
by CLooG.
struct clast_root {
struct clast_stmt stmt;
CloogNames * names;
};
struct clast_root *new_clast_root(CloogNames *names);
struct clast_assignment {
struct clast_stmt stmt;
const char * LHS;
struct clast_expr * RHS;
};
struct clast_assignment *new_clast_assignment(const char *lhs,
struct clast_expr *rhs);
struct clast_block {
struct clast_stmt stmt;
struct clast_stmt * body;
};
struct clast_block *new_clast_block(void);
struct clast_user_stmt {
struct clast_stmt stmt;
CloogDomain * domain;
CloogStatement * statement;
struct clast_stmt * substitutions;
};
struct clast_user_stmt *new_clast_user_stmt(CloogDomain *domain,
CloogStatement *stmt, struct clast_stmt *subs);
struct clast_for {
struct clast_stmt stmt;
CloogDomain * domain;
const char * iterator;
struct clast_expr * LB;
struct clast_expr * UB;
cloog_int_t stride;
struct clast_stmt * body;
};
struct clast_for *new_clast_for(CloogDomain *domain, const char *it,
struct clast_expr *LB, struct clast_expr *UB,
cloog_int_t stride);
struct clast_guard {
struct clast_stmt stmt;
struct clast_stmt * then;
int n;
struct clast_equation eq[1];
};
struct clast_guard *new_clast_guard(int n);
The clast_stmt returned by cloog_clast_create
is a clast_root.
It contains a placeholder for all the variable names that appear
in the AST and a (list of) nested statement(s).
A clast_assignment assigns the value given by
the clast_expr RHS to a variable named LHS.
A clast_block groups a list of statements into one statement.
These statements are only generated if the block option is set,
see Statement Block and CloogOptions.
A clast_user_stmt represents a call to a statement specified
by the user, see CloogStatement.
substitutions is a list of clast_assignment statements
assigning an expression in terms of the scattering dimensions to
each of the original iterators in the original order.
The LHSs of these assignments are left blank (NULL).
The domain is set to NULL if the save_domains option
is not set. Otherwise, it is set to the set
of values for the scattering dimensions
for which this instance of the user statement is executed.
Note that unless the noscalars option has been set, the
constant scattering dimensions may have been removed from this set.
A clast_for represents a for loop, iterating body for each
value of iterator between LB and UB in steps
of size stride.
The domain is set to NULL if the save_domains option is not
set. Otherwise, it is set to the set of values for the scattering dimensions
for which a user statement is executed inside this clast_for. Note that
unless the noscalars option has been set, the constant scattering
dimensions may have been removed from this set.
A clast_guard represents the guarded execution of the then
(list of) statement(s) by a conjunction of n (in)equalities.
Each (in)equality is represented by a clast_equation.
struct clast_equation {
struct clast_expr * LHS;
struct clast_expr * RHS;
int sign;
};
The condition expressed by a clast_equation is
LHS <= RHS, LHS == RHS or LHS >= RHS
depending on whether sign is less than zero, equal
to zero, or greater than zero.
The dynamic type of a clast_stmt can be determined
using the macro CLAST_STMT_IS_A(stmt,type),
where stmt is a pointer to a clast_stmt
and type is one of stmt_root, stmt_ass,
stmt_user, stmt_block, stmt_for or
stmt_guard.
Users are allowed to define their own statement types by
assigning the op field of the statements a pointer
to a clast_stmt_op structure.
struct clast_stmt_op {
void (*free)(struct clast_stmt *);
};
The free field of this structure should point
to a function that frees the user defined statement.
A clast_expr can be an identifier, a term,
a binary expression or a reduction.
enum clast_expr_type {
clast_expr_name,
clast_expr_term,
clast_expr_bin,
clast_expr_red
};
struct clast_expr {
enum clast_expr_type type;
};
void free_clast_expr(struct clast_expr *e);
Identifiers are of subtype clast_name.
struct clast_name {
struct clast_expr expr;
const char * name;
};
struct clast_name *new_clast_name(const char *name);
void free_clast_name(struct clast_name *t);
The character string pointed to by name is
assumed to be part of the CloogNames structure
in the root of the clast as is therefore not copied.
Terms are of type clast_term.
struct clast_term {
struct clast_expr expr;
cloog_int_t val;
struct clast_expr *var;
};
struct clast_term *new_clast_term(cloog_int_t c, struct clast_expr *v);
void free_clast_term(struct clast_term *t);
If var is set to NULL, then the term represents
the integer value val. Otherwise, it represents
the term val * var.
new_clast_term simply copies the v pointer
without copying the underlying clast_expr.
free_clast_term, on the other hand, recursively frees
var.
Binary expressions are of type clast_bin_type and
represent either the floor of a division (fdiv),
the ceil of a division (cdiv), an exact division or
the remainder of an fdiv.
enum clast_bin_type { clast_bin_fdiv, clast_bin_cdiv,
clast_bin_div, clast_bin_mod };
struct clast_binary {
struct clast_expr expr;
enum clast_bin_type type;
struct clast_expr* LHS;
cloog_int_t RHS;
};
struct clast_binary *new_clast_binary(enum clast_bin_type t,
struct clast_expr *lhs, cloog_int_t rhs);
void free_clast_binary(struct clast_binary *b);
Reductions are of type clast_reduction and
can represent either the sum, the minimum or the maximum
of its elements.
enum clast_red_type { clast_red_sum, clast_red_min, clast_red_max };
struct clast_reduction {
struct clast_expr expr;
enum clast_red_type type;
int n;
struct clast_expr* elts[1];
};
struct clast_reduction *new_clast_reduction(enum clast_red_type t,
int n);
void free_clast_reduction(struct clast_reduction *r);
CLooG provides static and dynamic version checks to assist on
including a compatible version of the library.
A static version check at compile time can be achieved by
querying the version constants defined in version.h:
CLOOG_VERSION_MAJOR
CLOOG_VERSION_MINOR
CLOOG_VERSION_REVISION
This way it is possible to ensure the included headers are of the correct version. It is still possible that the installed CLooG library version differs from the installed headers. In order to avoid this, a dynamic version check is provided with the functions:
int cloog_version_major(void);
int cloog_version_minor(void);
int cloog_version_revision(void);
By using both the static and the dynamic version check, it is possible to match CLooG's header version with the library's version.
Here is a basic example showing how it is possible to use the CLooG library,
assuming that a standard installation has been done.
The following C program reads a CLooG input file on the standard input,
then prints the solution on the standard output.
Options are preselected to the default values of the CLooG software.
This example is provided in the example directory of the
CLooG distribution.
/* example.c */
# include <stdio.h>
# include <cloog/cloog.h>
int main()
{
CloogState *state;
CloogInput *input;
CloogOptions * options ;
struct clast_stmt *root;
/* Setting options and reading program informations. */
state = cloog_state_malloc();
options = cloog_options_malloc(state);
input = cloog_input_read(stdin, options);
/* Generating and printing the code. */
root = cloog_clast_create_from_input(input, options);
clast_pprint(stdout, root, 0, options);
cloog_clast_free(root);
cloog_options_free(options) ;
cloog_state_free(state);
return 0;
}
The compilation command could be:
gcc example.c -lcloog -o example
A calling command with the input file test.cloog could be:
more test.cloog | ./example
First of all, it would be very kind to refer the following paper in any
publication that result from the use of the CLooG software or its library,
see Bas04 (a bibtex entry is provided behind the title page of this
manual, along with copyright notice, and in the CLooG home
http://www.CLooG.org.
This library is free software; you can redistribute it and/or
modify it under the terms of the GNU Lesser General Public
License as published by the Free Software Foundation; either
version 2.1 of the License, or (at your option) any later version.
This library is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU
Lesser General Public License for more details.
http://www.gnu.org/licenses/lgpl-2.1.html
Note, though, that if you link CLooG against a GPL library such as the PolyLib backend, then the combination becomes GPL too. In particular, a CLooG library based on the PolyLib backend is GPL version 2 only. Since the isl backend is LGPL, linking against it does not affect the license of CLooG.
CLooG can be used with one of two possible backends, one using isl and one using PolyLib. The isl library is included in the CLooG distribution, while the PolyLib library needs to be obtained separately. On the other hand, isl requires GMP, while PolyLib can be compiled with or without the use of GMP. The user therefore needs to install at least one of PolyLib or GMP.
To successfully install CLooG with the PolyLib backend,
the user first needs to install PolyLib
version 5.22.1 or above (default 64 bits version is satisfying
as well as 32 bits or GMP multiple precision version).
Polylib can be downloaded freely
at http://icps.u-strasbg.fr/PolyLib/ or
http://www.irisa.fr/polylib/. Once downloaded and unpacked
(e.g. using the `tar -zxvf polylib-5.22.3.tar.gz' command),
the user can compile
it by typing the following commands on the PolyLib's root directory:
./configure
make
make install
Alternatively, the latest development version can be obtained from the git repository:
git clone git://repo.or.cz/polylib.git
cd polylib
./autogen.sh
./configure
make
make install
The PolyLib default installation is /usr/local. This directory may
not be inside your library path. To fix the problem, the user should set
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/usr/local/lib
if your shell is, e.g., bash or
setenv LD_LIBRARY_PATH $LD_LIBRARY_PATH:/usr/local/lib
if your shell is, e.g., tcsh. Add the line to your .bashrc or .tcshrc (or whatever convenient file) to make this change permanent. Another solution is to ask PolyLib to install in the standard path by using the prefix option of the configure script: `./configure --prefix=/usr'.
CLooG makes intensive calls to polyhedral operations, and PolyLib functions do the job. Polylib is a free library written in C for the manipulation of polyhedra. The library is operating on objects like vectors, matrices, lattices, polyhedra, Z-polyhedra, unions of polyhedra and a lot of other intermediary structures. It provides functions for all the important operations on these structures.
To be able to deal with insanely large coefficient, the user will need to
install the GNU Multiple Precision Library (GMP for short) version 4.1.4
or above. It can be freely downloaded from http://www.swox.com/gmp.
Note that the isl backend currently requires GMP.
The user can compile GMP by typing the following commands on the GMP root
directory:
./configure
make
make install
The GMP default installation is /usr/local, the same method to
fix a library path problem applies as with PolyLib (see PolyLib).
If you want to use the PolyLib backend, then
PolyLib has to be built using the GMP library by specifying the option
`--with-libgmp=PATH_TO_GMP' to the PolyLib configure script
(where PATH_TO_GMP is /usr/local if you did not change the GMP
installation directory). Then you have to set the convenient CLooG configure
script options to build the GMP version (see Optional Features).
Once downloaded and unpacked (e.g. using the `tar -zxvf cloog-{No value for `VERSION'}.tar.gz' command), you can compile CLooG by typing the following commands on the CLooG's root directory:
./configure
make
make install
Alternatively, the latest development version can be obtained from the git repository:
git clone git://repo.or.cz/cloog.git
cd cloog
./get_submodules.sh
./autogen.sh
./configure
make
make install
Depending on which backend you want to use and where they are located, you may need to pass some options to the configure script, see Optional Features.
The program binaries and object files can be removed from the
source code directory by typing make clean. To also remove the
files that the configure script created (so you can compile the
package for a different kind of computer) type make distclean.
Both the CLooG software and library have been successfully compiled on the following systems:
gcc compiler,
gcc compiler,
gcc compiler.
The configure shell script attempts to guess correct values for
various system-dependent variables and user options used during compilation.
It uses those values to create the Makefile. Various user options
are provided by the CLooG's configure script. They are summarized in the
following list and may be printed by typing ./configure --help in the
CLooG top-level directory.
/usr/local:
make install will install the package's files in
/usr/local/bin, /usr/local/lib and /usr/local/include.
The user can specify an installation prefix other than /usr/local by
giving configure the option --prefix=PATH.
bundled together with CLooG.
Using the --with-isl option of configure
the user can specify that no isl,
a previously installed (system) isl or a build isl
should be used.
In the latter case, the user should also specify the build location
using --with-isl-builddir=PATH.
In case of an installed isl,
the installation location can be specified using the
--with-isl-prefix=PATH and
--with-isl-exec-prefix=PATH options of configure.
system) PolyLib, if any.
The installation location can be specified using the
--with-polylib-prefix=PATH and
--with-polylib-exec-prefix=PATH options of configure.
Using the --with-polylib option of configure
the user can specify that no PolyLib or a build PolyLib
should be used.
In the latter case, the user should also specify the build location
using --with-polylib-builddir=PATH.
configure. If the only existing version of the
PolyLib is the 32bits or if the user give to configure the option
--with-bits=32, the 32bits version of CLooG will be compiled. In the
same way, the option --with-bits=gmp have to be used to build
the multiple precision version.
configure will look for the GMP library
(necessary to build the multiple precision version) in standard
locations. If necessary, the user can specify the GMP path by giving
configure the option --with-gmp-prefix=PATH and/or
--with-gmp-exec-prefix=PATH.
The user can easily remove the CLooG software and library from his system
by typing (as root if necessary) from the CLooG top-level directory
make uninstall.
The CLooG distribution provides several documentation sources. First, the
source code itself is as documented as possible. The code comments use a
Doxygen-compatible presentation (something similar to what JavaDoc does for
JAVA). The user may install Doxygen
(see http://www.stack.nl/~dimitri/doxygen) to automatically
generate a technical documentation by typing make doc or
doxygen ./autoconf/Doxyfile at the CLooG top-level directory after
running the configure script (see Installing). Doxygen will generate
documentation sources (in HTML, LaTeX and man) in the doc/source
directory of the CLooG distribution.
The Texinfo sources of the present document are also provided in the doc
directory. You can build it in either DVI format (by typing
texi2dvi cloog.texi) or PDF format
(by typing texi2pdf cloog.texi) or HTML format
(by typing makeinfo --html cloog.texi, using --no-split
option to generate a single HTML file) or info format
(by typing makeinfo cloog.texi).